DOS-АТАКИ КАК КАТАСТРОФА «ЗВЕЗДА»
DOS-АТАКИ КАК КАТАСТРОФА «ЗВЕЗДА»
Аннотация
В статье рассматривается описание DoS-aтак с помощью теории дифференциальных уравнений потенциального вида с шестью управляющими параметрами. В правой части уравнения взят потенциал, который представляет катастрофу «звезда». Управляющие параметры отражают четыре наиболее эффективные способа защиты от DoS-aтак, а также производительность системы и входящий трафик. Скачкообразные смены стационарных равновесий – это катастрофы, которые могут ожидать компьютерную систему. Прогнозирование нежелательных катастроф состоит в отслеживание значений изменяющихся управляющих параметров. Опасными являются пересечения параметрами бифуркационных множеств. Продемонстрированы три проекции множества особенностей, позволяющие видеть, как меняется потенциальная функция и тем самым предсказывать возможные удачные хакерские атаки.
1. Введение
Атаки на сервер, известные под названием «отказ в обслуживании» (DoS-атака (от англ. Denial of Service)), доставляют много хлопот администраторам, и теоретически исследуются, как правило, в рамках понятий и терминологии теории компьютерной безопасности.
Когда осуществляется DoS-атака, то пользователи не смогут получить доступ к сайту или веб-сервису из-за их перегрузки. Происходит это в силу того, что для обслуживания запросов у сервера не хватает необходимой производительности, или в силу отсутствия соответствующей системы защиты установленной на сервере.
Напомним, что DoS-атаки на компьютерную систему осуществляются с другого компьютера, при которых происходят передачи данных. Как известно, для передачи данных используются семь уровней формирования данных для их передачи по физическому каналу связи, именуемых моделью OSI (Open System Interconnection model). Это прикладной, представительский, сеансовый, транспортный, сетевой, канальный и физический уровни. Каждый из них выполнят определенную функцию по передаче данных или по представлению их в том или ином виде для пользователя компьютера; каждому соответствует тот или иной набор протоколов передачи данных.
В статье была предложена математическая теоретико-катастрофическая модель DoS-атак, учитывающая все семь уровней модели OSI:
Здесь x(t) – число откликов сервера на запросы в момент времени t, τ – трафик и p – производительность сервера, p0 и τ0 – «типичные» характерные для данного сервера величины.
Два управляющих параметра t и p явно не отражают в полной мере ситуацию с работой сервера, который подвергнут DoS-атаке. Действительно, в этом случае единственной защитой от DoS-атак у нас будет наращивание производительности компьютерной системы. А это фактически означает техническое обновление системы и дополнительные финансовые затраты. Очевидно, что руководство далеко не всегда с этим согласится, и предложит решать проблему защиты за счет использования имеющейся квалификации персонала, обслуживающего сервер. В статье мы усложняем модель (1) за счет конкретизации способов защиты сервера от DoS-атак.
2. Переход к 6-параметрической модели
Физический уровень в модели OSI имеет дело с кабелями, модуляцией сигнала, кодированием и прочим. Проще говоря, физический уровень – это уровень проводов и физических способов передачи сигналов по проводам или с помощью беспроводной связи.
Поэтому более реалистичным кажется учет только шести уровней модели OSI, оставляющий без внимания физический уровень. В таком случае наша модель принимает вид
или
где
Но эта модель по-прежнему ограничивается самым примитивным способом защиты как наращивание производительности системы, как было отмечено во введении, т.е. ее обновлением. Очевидно, что нужно добавить в нее дополнительные управляющие параметры, которые отражали бы другие известные специалистам по отражению DoS-атак способы организации защиты сервера и которые были бы приемлемыми для владельцев сервера.
Рассмотрим следующую модель
где
l – управляющий параметр, отвечающий за блокирование через firewall превышения и настройку лимитов по количеству SYN-пакетов в секунду, которые вы ожидаете для вашего сервиса (защита от атак TCP SYN Flood) ;
u – управляющий параметр, отвечающий за отбрасывание пакетов, которые по ожиданиям будут слишком большого размера, чтобы не забивать оперативную память (защита от атак UDP Flood) ;
f – управляющий параметр, отвечающий за настройку firewall сервера: в политиках ни в коем случае нельзя оставлять настройки по дефолту. Важно закрыть все, кроме доверенных адресов и сетей ;
m – управляющий параметр, отвечающий за настройку мониторинга показателей сервиса: канал, загрузка CPU, траты памяти, работоспособности отдельных микросервисов и важных для бизнеса элементов сайта .
Эти параметры также учитывают не все способы защиты, но мы принимаем во внимание рекомендации специалистов, что «важно настроить мониторинг показателей сервиса: канал, загрузка CPU, траты памяти, работоспособности отдельных микросервисов и важных для бизнеса элементов сайта» .
3. Демонстрация 6-параметрической модели типа «звезда»
Предлагаемая модель (4) – это теоретико-катастрофическая модель типа «звезда» . Как правило, она подробно не анализируется в книгах по математической теории катастроф из-за сложности ее графического представления, за исключением монографии Вудкока и Постона , где даны различные сечения бифуркационного множества (см. ниже). Но приводимыми в этой книге графическими данными трудно воспользоваться на практике – они хороши лишь при теоретическом неторопливом анализе тех ли иных ситуаций. Работа сервера при DoS-атаках – это смена стационарных состояний. Опишем это подробнее.
Нормальная рабочая обстановка функционирования сервера – это стационарные состояния, при которых величина x(t) практически не меняется с течением времени t, т.е. имеем состояния, удовлетворяющие равенству
Смысл использования теории катастроф состоит в том, что при некоторых малых изменениях параметров l, u, m, p, τ могут происходить скачкообразные изменения числа откликов, т.е. возможны непредсказуемые резкие замены одного стационарного состояния на другое, что характерно для поведения компьютерных систем, подвергшихся DoS-атакам.
Для моделирования ситуаций на компьютере нам нужно визуализировать множество катастроф ΣV и множество особенностей CV функции V(x,a) соответственно
для рассматриваемой катастрофы «звезда» (4) и проекции C(x) на различные плоскости управляющих параметров a = (l, u, m, p, τ), получив так называемые бифуркационные множества, пересекая которые потенциальная функция V(x) будет изменяться: минимумы, соответствующие стационарным равновесиям, лежащим на ΣV, будут исчезать и образоваться новые, т.е. новые ситуации, в которых вынужден будет функционировать сервер (см. рис. 1-3), выдавая при этом соответствующее значение числа откликов x. Резкое падение x – это успешно проведенная атака. Поэтому важно знать, по каким путям изменения параметров можно прийти к стационарным равновесиям, в которых резко падает величина откликов x.
Очевидно, что некоторые переходы, смены состояний, могут восприниматься как нежелательные, а компьютерные эксперименты подскажут, изменение каких параметров опасно и чего надо избегать. В идеале было бы неплохо иметь установленное на сервере теоретико-катастрофическое программное приложение, которое в автоматическом режиме отслеживает состояние сервера, информирует о нем администратора и бьет тревогу, если близка опасная бифуркационная граница. На сегодня нам неизвестно существование такого приложение, а как выглядит визуализация проекций на плоскости (p, τ) (u, l) и (l, p) демонстрируется на рис. 1-3, полученных с помощью приложения, разработанного Е.О. Хлызовым в 2011 году .
На этих рисунках (в середине) даются проекции множества особенностей на ту или иную 2-мерную плоскость управляющих параметров, т.е. изображены бифуркационные множества. Цифрами помечены различные зоны на плоскости параметров, разделенные линиями бифуркационного множества, и приводятся графики функции V(x) соответствующие этим зонам. Минимумы отвечают стационарным состояниям, т.е. нормальным рабочим режимам сервера. Мы видим, что при переходах линий бифуркационного множества происходит исчезновения одних минимумов и появление других. Иначе говоря, мы видим смену рабочих режимов функционирования сервера.
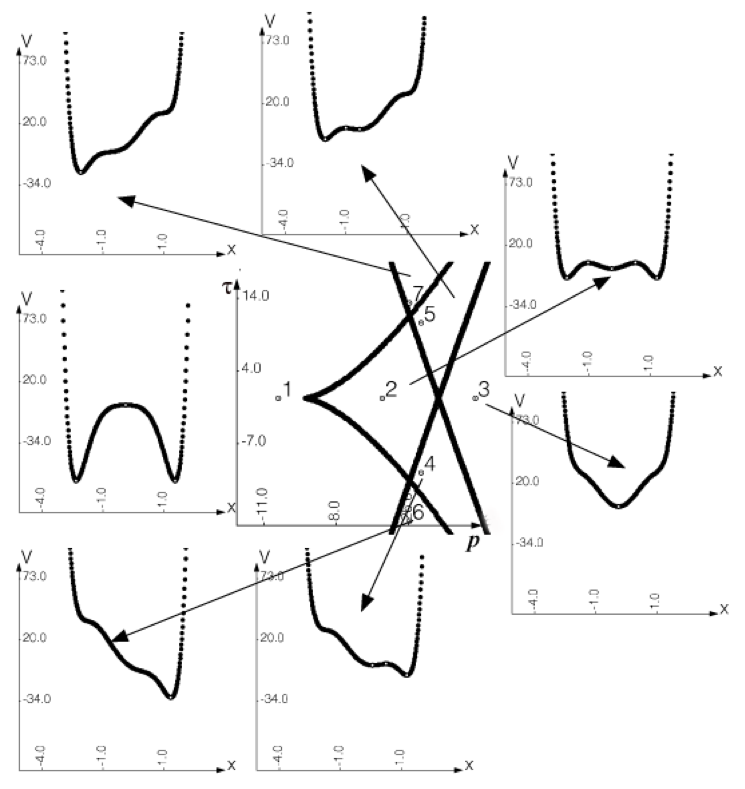
Рисунок 1 - Бифуркационное множество в проекции на (p, τ) и изменения функции V(x)
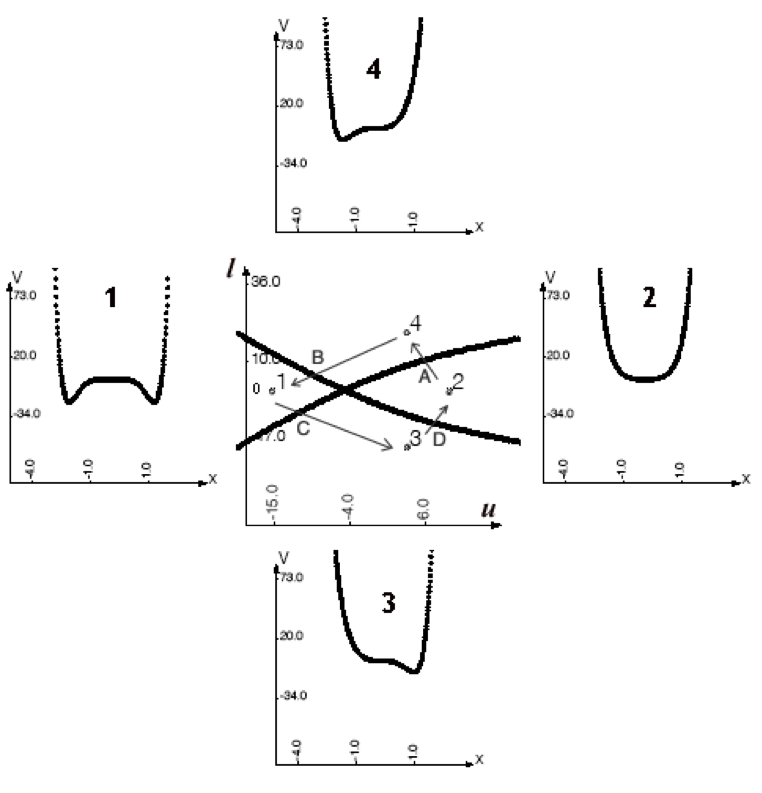
Рисунок 2 - Бифуркационное множество в проекции на (u, l) и изменения функции V(x)
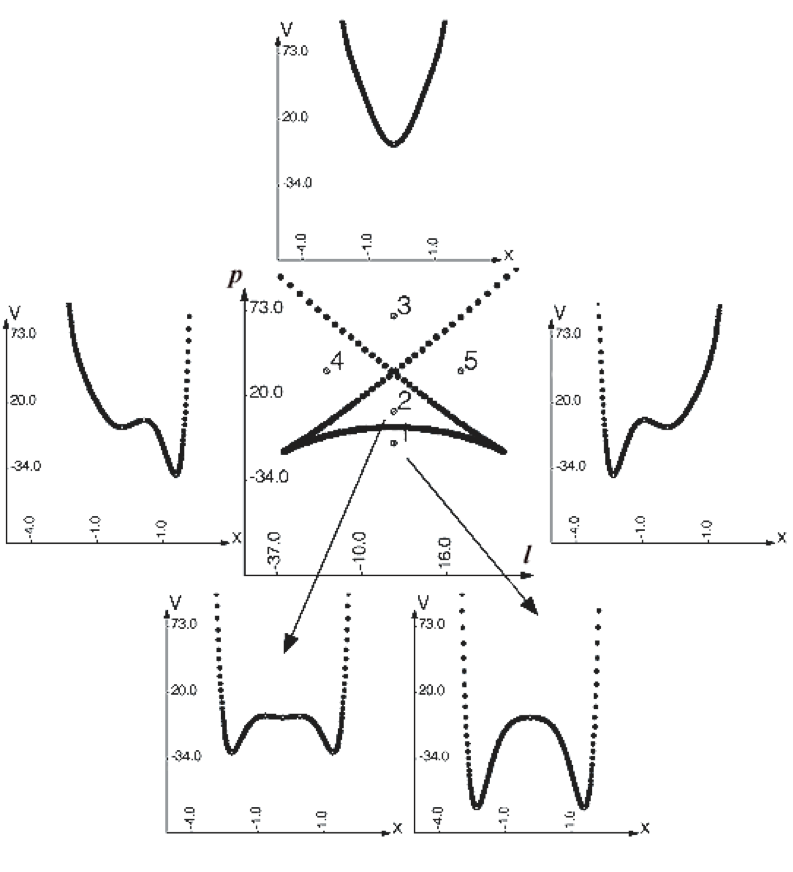
Рисунок 3 - Бифуркационное множество в проекции на (l, p) и изменения функции V(x)
4. Заключение
В статье мы предложили теоретико-катастрофическое описание DoS-атак, учитывающее шесть уровней модели OSI. В принципе, вместо OSI сейчас имеется в виду модель DoD (Department of Defence), которая пришла на смену модели OSI и содержит четыре уровня. Соответствующее теоретико-катастрофическое описание сводится к катастрофе «бабочка», которая проще, чем «звезда», и для нее имеются различные программные приложения. Тем не менее, изощренность хакеров известна, и иметь возможность проводить эксперименты по DoS-атакам с учетов всех уровней взаимодействия компьютерных систем более чем желательно. И, следовательно, разработка программного приложения, описанного выше, весьма актуальна.
