НЕПОЛНЫЙ АЛГОРИТМ В КОНСТРУКТИВНОЙ МАТЕМАТИКЕ (Часть 2)

Представлен способ порождения полного алгоритма.

Выделены и подвергнуты критическому анализу известные в науке операции: обращения и присоединения, введенные А.А. Марковым в теории алгоритмов

Навык (умение) алгоритма обнаруживать и классифицировать такую стрелку специального вида равносилен разделению (классификации) множеств по этому разделяющему признаку. Такие разделенные множества есть топосы

Это не способ переработки или способ вычисления (построения, обнаружения, конструирования) неизвестной, дополнительной части какого-либо алгоритма, а способ синтеза полного алгоритма, в котором строго показана эта дополнительная часть, которая впоследствии может стать неизвестной, а также некоторые категорные приемы работы с ней.

Порождающий полный алгоритм определен теоретико-категорно. Такой способ определения выбран по двум причинам, во-первых, теория категорий считается завершенной, во-вторых, такой же способ был использован в работах

Установлено, что теоретико-типовая проблема неполноты алгоритма связана с использованием типических последовательностей в качестве входных данных в алгоритм. При этом типические последовательности в алгоритме ведут себя так же, как введенные Брауэром беззаконные последовательности. Кроме того, те из них, что впоследствии образуют специальные последовательности, могут рассматриваться как один из частных случаев творческих последовательностей Брауэра.

Введение в рассмотрение подхода Брауэра к творчеству показывает способ переработки теоретико-типовых конструкций: как типических, так и специальных последовательностей, например, через «результат» А.Ш. Трулстра

Этот полученный научный результат не является очевидным, что показала практика применения типов в информатике, например, спецификаций, стандартов и протоколов типов известных языков программирования (например, стандарт

Проще говоря, не очевидно, что типы должны перерабатываться так же, как и «интуиционистские вычисления» по Трулстра — некоторым вычислителем (алгоритмом) с тремя типами входов. Причем эти входы параллельны, по аналогии с «интуиционистскими вычислениями», переработка типических последовательностей алгоритмом используется для корректировки переработки творческих последовательностей этим же алгоритмом.

Этот теоретический результат может быть применен в информатике. Почему важен «вычислитель Трулстра»? Допущение, принятое в первой части исследования, рассматривать классы P и NP как алгоритмы, и аналогичным образом типы как алгоритмы, приобрело конкретизированный вид алгоритма — вычислитель Трулстра. Синтезировать такой вычислитель непростая задача, её следует выделить в отдельную работу, возможно, показав его на более простом примере, нежели классы P и NP или типы. 

В настоящее время нет известных и широко признанных научных формализаций такого вычислителя, совершенно непонятно, какой алгоритм может его реализовать. Предполагается, что «на практике» (например, в каком-либо патенте) или «в информатике» (в какой-либо прикладной программе) кто-то мог получить такой вычислитель или приблизиться к его реализации. Но это станет ясно только после синтеза и обоснования его формулы. Синтез «вычислителя Трулстра» является актуальной научной и прикладной задачей, которую ещё предстоит осуществить.

Изыскиваются научно-технические пути формализации алгоритма искусственного интеллекта (ИИ), важными задачами при этом являются: теоретико-типовая по корректной переработке типов, точнее уточнение формализации типов, такой, что не содержит в своем составе типов, которые перерабатываются неполно, а также теоретико-алгоритмическая по синтезу полного алгоритма.

1.1. Структура исследования

Исследование представлено в двух частях. В первой части были представлены результаты исследования теоретико-типовых причин неполноты алгоритма. Во второй части представлен способ порождения полного алгоритма. 

2.1. Операции в алгоритме Маркова

В нормальном алгоритме Маркова определены, помимо, слов и однонаправленной стрелки (знака препинания), две операции: обращения и присоединения.

Эти операции хорошо иллюстрируют проблему грамматики над алфавитом.

Существо этой проблемы грамматики состоит в том, что буквы в разных естественных языках присоединяются друг к другу и образуют слова не случайным или хаотичным образом, а согласно правилам и грамматике этого языка. Но и сами слова и грамматики образовались не случайно, в них много общего в различных естественных языках. Фундаментальное и общее свойство всех людей, вне зависимости от их естественного языка, состоит в том, что они наделяют словом некоторый объект окружающего их мира, выделяя и воспринимая этот объект интуитивно и одинаково. Существуют, конечно, исключения из правил, но в подавляющем большинстве случаев это так. Аристотель смог обобщить слова, выделив категории, которые более полно представляют способы наделения объекта словом и понять сам принцип синтеза этих способов, который оказался логичным, как интуитивно, так и строго математически. Далее категории Аристотеля уточнялись, но принцип сохранился и сегодня, поэтому в научном обороте корректно общезначимое обобщение — аристотелевы категории.

Маркову пришлось отдельно определить простейшую грамматику, позволяющую составлять из букв, читай типических последовательностей, слова — специальные последовательности. Но саму грамматику, например, как внешний или внутренний морфизм между буквами, возможно тайный, не определил. Поэтому его слова «технически» существуют, но не принимается во внимание, что кто-то их отдельно определил.

При этом Марков строго математически определил такой «упрощенный» способ словообразования: буквы просто присоединяются друг к другу, образуя слово и имеется возможность циклически сдвинуть буквы относительно некоторой «начальной». Как и кем запускается процесс присоединения, как он останавливается, не принимается во внимание, некоторое управление существует, но не известно алгоритму. Поэтому, например, когда необходимо при помощи нормального алгоритма Маркова составить не слово некоторого нового, ранее не известного, а наоборот известного, естественного языка, то кто-то должен составить «правильную» последовательность присоединения букв и сообщить её алгоритму.

По существу, это уловки Маркова (Марков — брат, но истина дороже), которые должны были вызывать обоснованные сомнения на этапе их защиты в составе рассуждений теории.

Сами рассуждения Маркова содержательны и прогрессивны.

Поэтому заметим, что эти операции представимы также стрелками, причем эти стрелки обозначают обособленные морфизмы в терминологии, введенной в работах

Т.е. такие, что способ выполнения их предписания единственен. Тогда в нормальном алгоритме Маркова можно было определить три стрелки, а не одну, нарисовав их, например, «красиво» или «вычурно» дабы отличать от однонаправленной стрелки!

Таким образом, вместо способа формализации полного алгоритма научной общественности Марковым был продемонстрирован частный случай неполного алгоритма!

2.2. Операция «аппликации» Алонсо Чёрча

Операция аппликации (прикладывания, присоединения), введенная А. Черечем в λ-исчислении, трактуется как алгоритм вычисляющий результат по заданному входному значению и записывается как ƒ a, что соответствует традиционной в «классической» математике и теоретико-множественном, наивном подходе записи ƒ (a).

Однако имеется крайне «неприятная оговорка»: «в этом смысле аппликация может рассматриваться двояко: как результат применения  ƒ к a, или же как процесс вычисления этого результата». В первом смысле операция аппликации — это стрелка (морфизм) со значением, во втором, алгоритм.

В науке известно, что логика высказываний соответствует простому типизированному λ-исчислению, логика высказываний второго порядка — полиморфному λ-исчислению, исчисление предикатов — λ-исчислению с зависимыми типами.

Рассмотрим внимательно конструкцию ƒ к a.

Можно ли подставить вместо ƒ группы переменных — нет, в место a – можно.

Во-первых, такие ничего не значащие буквы, как  ƒ  применяются в математике, во-вторых, с позиций конструктивной математики таковые весьма «опасны», так как нет способа обнаружить и распознать ƒ среди других таких же ƒ, а если такой способ есть, то возможно, что он оперирует не всеми классификаторами, а их возможные композиции существенно влияют на конечный результат. Это очень специфическая математическая конструкция, которую далее покажем в известной теории, в которой способы работы с ней являются наглядными, понятными и безопасными так как о такие буквы можно разделять между собой по формуле правой части.

В работе

Из работы

где:

XY — объекты;

ƒ — морфизм (стрелка);

a — значение морфизма.

значительно выразительнее конструкции Чёрча: ƒ a, так как дополнительно оперирует словами, а конструкция вида

где typeK — ассоциатор морфизма, есть доопределённая поƒ через typeK.

Обратим внимание, на то, что выше выделено слово: соответствует, т.е. имеется некоторая конструкция: ƒ a⤖Z, где «⤖» — это морфизм, буквально означающий соответствует высказыванию Z тогда можно определить и ƒ a⤗Z, где «⤗» — несоответствует. Здесь морфизм ƒ a — это теоретико-n-категорный ассоциатор морфизма «⤖», высказывания Z, где Z — пропозиционная (proposition — лат.) переменная. Покажем такую конструкцию иначе, например, как: 

Таким образом, «просто доопределить по typeK» конструкцию Чёрча не получится. В формуле: 

Также некоторые из морфизмов ƒ, определённого типа typeK для двух объектов X, Y всегда будут приводить к зацикливанию алгоритма, перерабатывающего такую формулу, для других никогда или редко, например, в зависимости от конкретизированных объектов X, Y, для других таких пар объектов всё будет иначе.

2.3. Операция «обрезания» Воеводского

В работе

Следуя выше приведенной логике, в отношении операций, обозначим операцию обрезания (truncation) Воеводского специальной, «вычурной» стрелкой «⤞». Эта стрелка есть волюнтаристское решение на совершение отдельного предписания алгоритма.

Положим, что для стрелки такого вида – это решение может быть подтверждено «как правильное», при каких-либо ограничениях. Определим также стрелку, когда такое решение может быть подтверждено как «не правильное»: «⥇». Запишем общие категорные формулы такой операции:

(1)

(2)

(3)

(4)

где:

C – это некоторая категория, в теоретико-категорном смысле;

Z – слово или в общем случае высказывание.

Здесь можно было бы и не писать категорию C, а показать простое множество в теоретико-множественном смысле, но не хотелось бы упрощать идею Воеводского, так как таковая может быть показана, как в теоретико-множественном, так и теоретико-категорном подходе, поэтому выбран второй, старший подход.

Кроме того, если подставить множество, то может оказаться так, что будут повторены выводы об операции аппликации А. Чёрча, показанные выше.

2.4. Буквы беззаконны по Брауэру

Этот подзаголовок можно завершить как вопросительным, так и восклицательном знаком. Проведем мысленный эксперимент в «стиле» Л.Э.Я. Брауэра:

«Пусть:

1. Имеется алфавит из букв.

2. Определена однонаправленная стрелка, позволяющая присоединить одну букву к другой.

Допустим, что буквы алфавита присоединяются друг к другу в произвольной последовательности, при этом длина слова ничем не ограничена.

Среди букв нет известных наблюдателю.

Тогда среди полученных слов также нет известных.

Все такие слова беззаконны, аналогично значению морфизма измерителя (датчика)».

2.4.1. Слова по Брауэру, полученные в результате творчества

Продолжим мысленный эксперимент:

«Пусть:

1. Алфавит состоит из известных букв.

2. Определена однонаправленная стрелка, позволяющая присоединить одну букву к другой.

Допустим, что буквы алфавита присоединяются друг к другу в произвольной последовательности, при этом длина слова ничем не ограничена.

Тогда среди всех слов будут такие, что известны в некотором словаре, а также такие, что неизвестны.

Наметился некоторый процесс творческого перебора комбинаций букв такой, что этот процесс может закончится успехом или неудачей. Положим, что если слово известно, то это успех. Обозначим такой успех специальной стрелкой «⤇», неудачу – «⤃».

C⤇Z (3)

C⤃Z (4)

где:

C – это некоторая категория;

Z – слово или в общем случае высказывание.

2.5. Конкретизация задачи

Заметим, что формулы (1), (2) и (3), (4) – «похожи», хотя описывают различные математические объекты, формулы (1) и (2) теоретико-типовые конструкции, формулы (3) и (4) логические, интуиционистские, теоретико-алгоритмические.

Необходимо определить возможность и основу для обобщения над ними, тем более, что такая практика широко распространена в математике в виде метафор (обобщений над непознанными классами): «подобны», «соответствуют», «эквивалентны».

3.1. Тип «Boolean»

Запишем категорные формулы этого типа, обозначив категорию истинности как понятие, содержащее вывод высказывания Z на естественном языке: «Истинно», обозначив стрелкой «⇒» успех достижения «Истинно», а стрелкой «⇏» неуспех достижения этого значения.

C⇒Z

C⇏Z

Заметим, что здесь некоторое «отождествление», «эквивалентность», «подобие» слова естественного языка «Истинно» и некоторого объекта окружающего нас мира C, в отношении которого допущено, что этот объект, представимый категорией, можно сжать и закодировать словом, показан через взаимодействие (взаимосвязь, действие, морфизм, специальную вычурную стрелку). Эта стрелка может быть потенциально реализуемой не всегда, во-первых, в том случае, когда объект окружающего нас мира изучен с приемлемым, текущим уровнем знания о нем, во-вторых, такое знание может быть пересмотрено в дальнейшем, в-третьих, оба эти знания можно характеризовать некоторых отрезком времени, когда таковое существует, в-четвертых, для искусственных миров, где сами эти объекты могут быть и противолежащими.

Положим, что Z — это не только слово, но и цифра, например, 24, может быть строка символов, например, 24 В, но может быть одновременно и другая цифра например «единица» в какой-либо системе исчисления, например, двоичной, возможно это также цифра к которой дополнительно приложена какая-либо кодовая таблица T (например, код МТК-2, на базе которого разработаны коды КОИ-7 и КОИ-8, или UNICOD), т.е. в общем случае — ассоциатор, обозначим его красивой буквой

например, как описано:

Это формальное представление беззакония типов, оно же известно в науке под другими названиями, например, — кодирование, оно же уникальное кодирование, оно же таблица замен, оно же перевод с одного искусственного языка на другой такой искусственный язык без должного основания. Пусть здесь не смущают слова естественного языка, так как таковые в математическом смысле — беззаконны. Фактически — это известный всем уникальный шифр.

Предположим, что идея учинить математическое «беззаконие» противоречит целям любых теорий, в том числе и типов, однако как математически, так и эвристически — на уровне приведенного примера понятно, что беззаконие типов широко распространено в информатике.

Все показанные выше примеры типичны без учета

Очевидно, что Z, V, W можно переставить так, чтобы привести такое «отождествление» к абсурду, породив парадокс, в частности типических последовательностей, такой парадокс назовем «парадоксом Мартина-Лёфа».

Наличие парадокса требует поиска путей его преодоления, традиционным путем может выступить аксиоматизация и построение категорной логики, где все такие «отождествления» будут полагаться слабыми n-категориями, имеющими различный логический смысл, при разном положении ассоциаторов

Следует принять, ранее введенный тип морфизма typeK как некоторую композицию стрелок, где некоторые из них есть стрелки стрелок — морфизмы морфизмов — ассоциаторы, определив typeK как слабую n-категорию, которая при определенных условиях может стать сильной n-категорией, если для неё удастся определить только ассоциативные композиции.

Далее будем понимать тип морфизма typeK именно так, более не возвращаясь к его существу.

3.1.1. Способ порождения полного алгоритма

Представим выборки входных данных в виде теоретико-категорной формулы.

Положим, что на вход алгоритма поступают типические последовательности.

Предположим, что некоторый алгоритм способен породить предписания, которые потенциально могут переработать такие входные выборки данных.

Здесь введено предложение рассмотреть «способность алгоритма породить предписания переработки», при этом совершенно неясно, что будет, если таковые удастся породить, алгоритм сможет переработать данные или нет?

Обозначим C буквой  — категорию, следуя теоретико-категорной традиции.

Определим формулу категории, также следуя принятым правилам:

где:

μ — морфизм, он же показан стрелкой;

XY — объекты, т.е. традиционно для теории категорий, здесь не привносится никаких новых подходов.

Объекты XY определим как слова в алфавите Маркова A = X,Y,Z,… — этот способ определения объектов отличает настоящее исследование.

Введем в эту формулу (5) ассоциатор typeK через терм «:» — это категорный ассоциатор типа морфизма, тогда:

(6)

Введем значение морфизма буквой a — это переменная (используем букву, которая была показана ранее при анализе результатов А. Чёрча).

Получим формулу вида:

(7)

Способ, который применен для определения ассоциаторов традиционен для теории n-rкатегорий, запись через терм «:» — новаторство, для краткости, т.е. для того, чтобы не строить стрелку над стрелкой, термы читаются слева на право, например, для формулы (7), как стрелка typeK над стрелкой μ, где таковая стрелка над a.

Определим вывод, который нельзя считать нормальным по Маркову в категории C:

(8)

где:

MSM – малые морфизмы;

знак «/» разделяет терминальные и нетерминальные символы языка;

буквы:

Сами морфизмы, при этом, рассматриваются как π – начальные, ε – обычные и η – заключительные марковские вхождения в алфавите Маркова 

Покажем, что категория CM может взаимодействовать с другими категориями, т.е. слева и справа в неё имеются морфизмы в том же алфавите M – это:

Обозначим множество категорий пронумеровав их последовательно, по мере поступления из выборки входных данных, как 1,2,3,…,x, здесь все буквы справа от равно переменные, допускающие подстановку групп переменных:

(10)

Морфизмами с одной стороны от CM , читай теперь как CMx, пренебрежём, так как на настоящем этапе формализации, способ приема, фильтрации, аналогово-цифрового преобразования не вызывает интереса. Сторона, где не будут рассматриваться морфизмы зависит от выбранного направления индукции, получим:

Пустота λ с одной стороны от категори CMx несколько упростит дальнейшее понимание преобразований. Обозначим категорию всех таких категорий как 

где:

λ в верхнем индексе буквально обозначает, что вокруг этой категории λ – пусто;

предписание x – эндоморфизм в CMx, равносильный просто букве: CMx, записанный как теоретико-категорный морфизм, иначе говоря, как: 

Сама такая категория 

Можно ли подставлять вместо переменных M,x группы переменных – можно, можно ли тоже самое делать с переменной C – нет, для корректной подстановки переменных вместо C, необходимо вернуться в алфавит A, C буква здесь дань теоретико-категорной традиции (так понятнее многим) и буквальное предписание заменить (заместить) буквы алфавита A и их морфизмы (стрелки) общим обозначением C – единственной буквой, для краткости;

Рассмотрим возможности категории: 

Тогда, конечно, объекты D1…D5, можно дополнительно конкретизировать с учетом стрелок.

Например, в промышленной автоматизации принято рассматривать два таких направления: слева-направо и справа-налево, и обозначать соответственно: DI1 и DO1, но теоретически универсальным будет обозначение: DM1, DM2, DM3,…

Формула: 

При  «неслепом приеме (переработке данных)» априори известна некоторая категория, которая позволяет «понять», что делать с 

Представить себе такие категории можно, показав некоторую упрощенную структуру для дополнительного алгоритма 

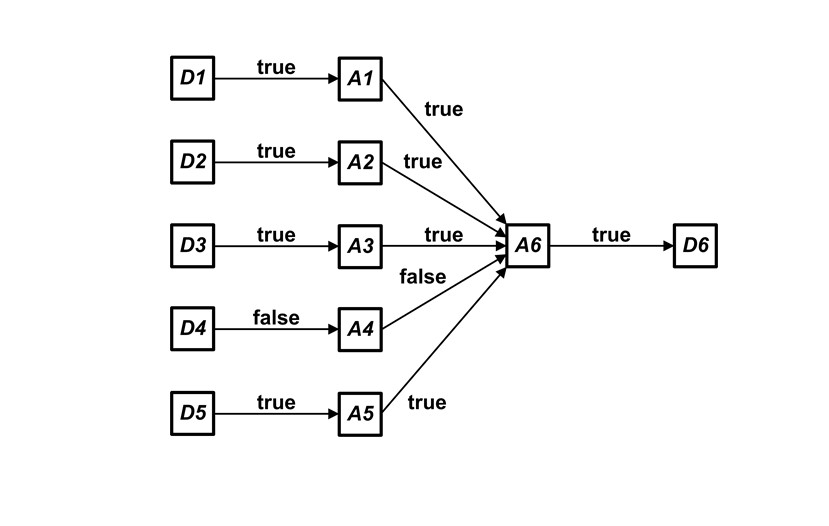
Рисунок 1 - Пример композиции CMx и CMU

DOI:10.60797/itech.2026.9.1.1

где:

D1, D2, D3, D4, D5, D6, A1, A2, A3, A4, A5, A6 – слова;

«→» – стрелка – обозначение морфизма;

true,false – значение морфизма.

Также придется вернуться к записи 

Проше говоря, во всех формулах, где есть C, показывается некоторый конкретизированный набор морфизмов, читай некоторая сигнатура категории, поэтому постоянно приходится уточнять, что именно в верхнем индексе при C.

Зададимся вопросом: «Известна ли категория 

Это зависит от позиции наблюдателя, если наблюдатель – разработчик, то он определяет 

Например, имеется возможность наблюдения за техпроцессом, читай морфизмами, показанными на рисунке 1, пусть к ним добавлен морфизм 

Очевидно, что «неочевидные» морфизмы A1, A2, A3, A4, A5 → A6 дублируют морфизмы D1→A1, D2→A2, D3→A3, D4→A4, D5→A5, и имеют «техническое» назначение.

Заметим, что (13) – это полноценная категорная формула, причем таковая действительно имеет место быть в объектах окружающего нас мира, где:

Но, тогда получается, что A1, A2, A3, A4, A5 входят в состав обеих категорий 

Именно так, можно показывать формулу (14) открытую справа в алфавите M, т.е. не включая A1, A2, A3, A4, A5, но это не верно, как математически, так и технически. Технически, если положить, что 

Формула (14) – это простой пример дополнительного, скрытого алгоритма, дополняющего неполный алгоритм до полного.

Реальная формула алгоритма 

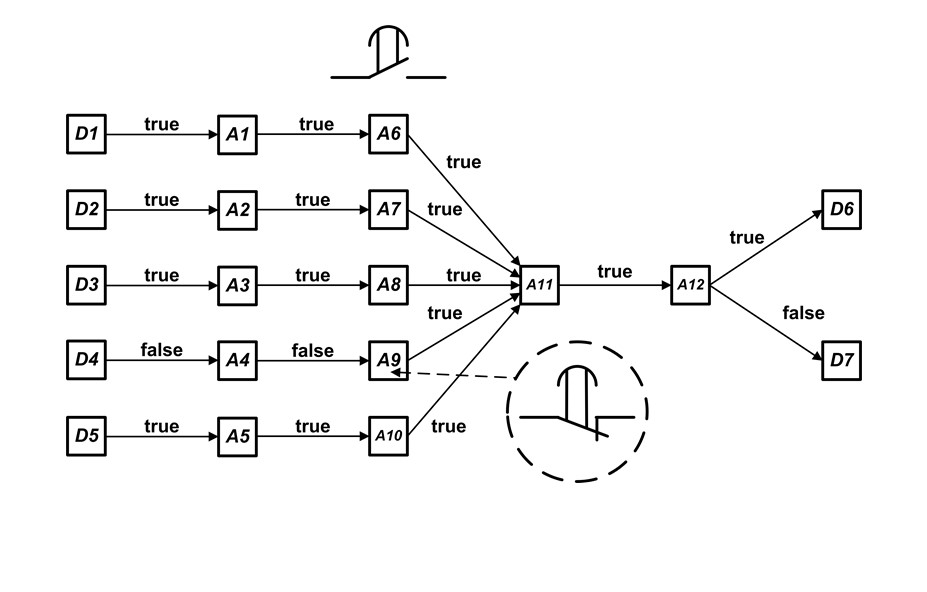
Рисунок 2 - Пример композиции CMx и CMU более сложной категории

DOI:10.60797/itech.2026.9.1.2

где:

D1,…,D7, A1,…, A12 – слова;

A6, A7, A8, A10 – замыкающие контакты реле времени с задержкой при срабатывании показаны сверху над схемой стандартным обозначением;

A9 – размыкающие контакты реле времени с задержкой при срабатывании, показан в круге с пунктирной линией;

A12 – можно представить как слово ошибок, если таковое равно нулю, то ошибок нет и вывод D6, не равно нулю – ошибки есть – вывод D7.

Сам техпроцесс можно себе представить, как трубопровод с запорными клапанами, где D4, A4, A9 – байпасный трубопровод, а задержка во времени обусловлена возможной различной длиной трубопровода на разных инженерных объектах, при сохранении для них всех общего алгоритма, тогда задержки выставляются дополнительно для каждого такого объекта, в зависимости от реальной протяженности трубопроводов (для разных архитектурно-строительных решений на объектах).

Это пример (рисунок 2) также относительно прост, хотя и сложнее, представленного на рисунке 1.

В формулу (13) довольно легко и без объяснений был добавлен вывод A6 → D6, потому, что таковой наблюдаем, т.е. известен всем возможным наблюдателям, но его «отождествить» с категорией CMx можно только в некоторых простых случаях.

Попробуем «отождествить» интуитивно. Будем помнить, что «отождествить» без знания 

Таковой незаконен так как кажется и не более, что волюнтаристские действия обоснованы, ведут к осмыслению 

Какова возможная альтернатива для такого волюнтаризма – это полный перебор, т.е. имеет место быть случай неравенства классов P и NP, но только для одного из наблюдателей. Для наблюдателя-разработчика классы P и NP по-прежнему равны, т.е. проблема: «равенства классов P и NP» (проблема перебора)» относительна (и относительно наблюдателя).

Причем имеет место быть только для наблюдателей не знающих

Например, наблюдатель-шифровальщик мог просто скрыть часть алгоритма, отвечающую за генерацию типических последовательностей, например, придумав и скрыв ключ шифрования. Вернемся к примеру, показанному на рисунке 1.

Можно представить, что между A1, A2, A3, A4, A5 →⋯→⋯→ A6 имеются совершенно неизвестные фрагменты для наблюдателя – потребителя, тогда формула (13) для него будет выглядеть так:

где ему известны CMx и Z, а все морфизмы до Z «кажутся» (предполагаются) «неассоциативными», т.е. для него это слабая -категория, а категория 

Что удалось получить в формуле (13), новый алгоритм переработки?

Нет в этой формуле получен способ порождения полного алгоритма и показан для неё неполный алгоритм. Перерабатывать данные по категорной формуле (13) алгоритм сможет только, если известна её правая часть, но проблема состоит в том, что частично известна левая.

Таким образом, явно обозначилось деление алгоритмов, как минимум, на порождающий и перерабатывающей. Очевидно, что можно принять во внимание способ модернизации этих алгоритмов, а также способ анализа, или подбора, или перебора, или взлома дополнительного, скрытого алгоритма в составе порождающего, тогда имеет смысл включить в общую формализацию алгоритмов разделяющий признак назначения: порождающие, перерабатывающие, модернизирующие и вскрывающие.

Учет разделения алгоритмов в их общей научной формализации позволит более корректно и точно рассматривать проблему «равенства классов P и NP» (проблему перебора)», так как таковая свойственна не всем из них и зависит от позиции наблюдателя.

3.2. Методика определения стрелок в формулах (1-4) и (15)

Из способа определения полного алгоритма следует, что для обобщения над формулами (1), (2) и (3), (4) необходимо математически определить:

1. Полный алгоритм.

2. Наблюдателей.

3. Наблюдаемую часть алгоритма CMx.

4. Дополнительный алгоритм

5. Наблюдаемый вывод.

6. Предположение о дополнительном алгоритме

7. Определить typeK как типическую последовательность или напротив, как специальную.

8. Абстракцию «точный вывод».

Как только это наблюдаемый вывод будет определен, то его можно подставить в формулы (1), (2) и (3), (4) вместо переменной Z.

Ввести:

– переменную для наблюдателей, например, автор – author и слепой – blind;

– заменить все, ранее использованные, «вычурные» стрелки одной, единственной такой стрелкой, например, «⤳»;

– переменную для «точного вывода», например, обозначив буквой W, выбрав её значение «нейтральным» для любого алгоритма, например, "Работаю" (это сделано для упрощения, в прикладных задачах эта буква может быть заменена группой переменных);

– переменную для подмены

– переменную для типической последовательности, например, ТП.

Показать подмену, например, так:

(16)

Но такого представления, как показано в формуле (16) недостаточно, необходимо показать как конкретно получена 

(17)

Тогда формулу (17) можно приложить к аппликации А. Чёрча, получив более конкретизированный вид для ƒ. В правой части этой формулы применяется такая же бессмысленная буква C, однако вместо неё можно подставлять слова и морфизмы по формулам (8) и (10), определив их как X, Y в алфавите Маркова и использовав служебный алфавит M для кодирования стрелок с выводом, который нельзя считать нормальным по Маркову, получив:

(18)

В формуле (18) буква ƒ, введенная Чёрчем, определена для всех наблюдателей. Алгоритм 

Формула (18), в том числе, показывает данные, которыми будет оперировать «вычислитель Трулстра». Такой вычислитель возможно синтезировать. Для его синтеза необходимо классифицировать категории, т.е. приложить комплекс классификаторов, способных переработать входные данные вида: 

где M – служебный алфавит, вывода, который нельзя считать нормальным по Маркову, а MK также служебный алфавит, такого же вывода, но используемый в канале управления cNne–схемы алгоритма Маркова, по существу – множества, в категории с классификатором – топосы.

Так как переработать необходимо фактически систему (18), т.е. структуру у которой предполагается наличие нескольких входов и возможно нескольких выходов, то необходим и соответствующий ей алгоритм, например, такой как показан в работах

Предложение приложить именно cNne–схемы алгоритма Маркова и, как следствие сеть Маркова непрямого распространения, в качестве «вычислителя Трулстра» – является новаторством. Однако, пока, не предложено какой-либо научно обоснованной альтернативы. Появление таковой в научном обороте позволит сравнить подходы, с предложенным здесь, пока провести такое сравнение не с чем. Поэтому cNne–схема алгоритма и сеть Маркова непрямого распространения показаны как реализуемый (конструктивный) способ переработки формулы (18).

3.3. На сколько типы морфизмов применимы в алгоритме ИИ?

Можно заметить, что человеческий интеллект не получает данные от своего организма в вольтах или амперах, целым значением или с плавающей точкой, тем более тип, составленный из них, и это незнание не мешает ему мыслить. Отсюда следует первое наблюдение – тип не нужен человеческому интеллекту, чтобы функционировать.

Однако, человеческий интеллект пытается оценить объекты окружающего его мира и интуитивно разделяет их первоначально на «классы», выделяет в них «свойства», пытаясь обобщить и сформировать «первое» представление об объекте и его возможных взаимодействиях (морфизмах).

При этом «классы» и «свойства» выступают некоторыми прообразами будущего представления об объектах и их морфизмах. Далее человек пытается зафиксировать «классы» и «свойства» словами, ввести для них меры. Потом убеждается, что не все «классы», «свойства», «меры» одинаковы, но есть такие, что для них можно ввести «тип», использовав букву, или слово, или их композицию, и поделиться этим «типом» с окружающими. Такой подход свойственен всем людям.

В настоящее время, благодаря науке, этот простейший человеческий опыт обобщен и формализован. В реальном мире человек опирается на уже известные такие «типы», сообщенные ему предками, становясь ученым, берет их под сомнение, совершенствует, пересматривает и сообщает об этом другим людям. Поэтому «типы» естественным образом начинают сопровождать его с самого рождения.

По-видимому, такой же процесс будет ожидать и ИИ, но его можно упростить, сообщив ему только такие из них, что перерабатываются дедуктивными методами и, например, не приводят к зацикливанию алгоритма, а если приводят к таковому, то это может быть преодолено.

Формула (18) — это более строгое определение равенства или неравенства классов P и NP. В ней же показаны: равенство таких классов для наблюдателя author, причина неравенства этих классов — типические последовательности для наблюдателя blind, а также продемонстрирован путь «перебора» с творчеством Л.Э.Я. Брауэра.

«Беззаконие» в теориях алгоритмов и типов «учинили»: А.А. Марков и П.Мартин-Лёфф, добавил такового в теорию типов В.А. Воеводский, работы А. Тьюринга и А. Чёрча нет смысла рассматривать в этом контексте, так как они достаточно далеко отстают от существа этой проблемы.

Это важное замечание в теориях алгоритмов и типов, так как необходимо быть внимательным к рассуждениям о творчестве Л.Э.Я. Брауэра, по-видимому, таковые имеют куда как более глубокий смысл для формализаций этих теорий.

«Мягкие» творческие действия в формуле (18) представимы слабыми категориями

Проще говоря, с этими ассоциаторами должна быть полная ясность, необходимо сформировать полный перечень таковых и алгоритм Uovercoming, который может строго и обосновано математически «подключить» или «не подключать» таковые в процессе выполнения предписаний.

Однако это ещё не всё, что замечено в рассуждениях Брауэра и «беззаконных» операциях: Чёрча, Маркова и Воеводского. Что-то необходимо предпринять со всеми этими «вычурными» стрелками: «⤳», «⤖», «⤇», «⤞».

Например, на практике эти стрелки «беззаконно» отождествляют, считают эквивалентными, подобными, похожими на какую-либо простую стрелку, это хорошо видно в работе Воеводского и известном соответствии (изоморфизме) Карри-Ховарда, они как бы бросают вызов фундаментальной идее Брауэра и всей интуиционистской логики исключения из рассуждений «Закона исключенного третьего», ведь отождествить или поставить в соответствие некоторой «сложной» интуиционистской логике можно булеву алгебру, намеренно и волюнтаристски «загрубив» вывод, например, до показанного в (18) — "Работаю".

В современных прикладных задачах, в частности, в промышленной автоматике такое «беззаконие» и волюнтаризм широко распространены, при этом «катастрофы вселенского масштаба» не произошло, заводы и фабрики работают, алгоритмы, введенные в автоматику таких предприятий, функционируют, а когда «третье все же оказывается дано», то в дело вступает ремонтный персонал и творчество Брауэра, следовательно, можно сделать вывод, что так делать (поступать) можно.

Открытым, дискуссионным, научным вопросом является «узаконивание» таких отождествлений, а также более строгая их формализация (определение четких «правил игры»).

Проще говоря, алгоритм должен понимать, что какой-либо из его выводов намеренно загрублен и включать в свой состав контр-алгоритм противодействия или минимизации ущерба от такового, например, в той же промышленной автоматизации известен алгоритм «преодоления дребезга электрических контактов», вполне себе понятный и используемый, а также «аварийные цепи» и подсистемы безопасности персонала.

Все эти рассуждения важны для будущей формализации алгоритма ИИ.

 4.1. Выводы

Предложение приложить вычислитель Трулстра к типам является новаторством.

Такой способ переработки современных типов в известных теориях типов более адекватен введенным в них теоретическим допущениям. Соответственно, применяемые в настоящее время способы и приемы переработки типов, опирающиеся на эти теории, менее адекватны.

В этом вопросе нет расхождения между теорией и практикой, просто на практике сложилась некоторая «традиция» применения теоретико-типовых положений, которую целесообразно уточнить.

Теоретико-типовые рассуждения и следующие из них научные выводы и прикладные способы применения научных результатов не должны приводить к «проблемам» в алгоритме. Наличие «проблем» в алгоритме должно рассматриваться научным сообществом как основание к критическому взгляду на предлагаемые теории типов.