USING A SELF-ADAPTIVE EVOLUTIONARY ALGORITHM TO SOLVE THE TRAVELLING SALESMAN PROBLEM
USING A SELF-ADAPTIVE EVOLUTIONARY ALGORITHM TO SOLVE THE TRAVELLING SALESMAN PROBLEM
Abstract
The travelling salesman problem is a classical NP-complete combinatorial optimisation problem. One of the well-known ways to solve it is genetic algorithms (GAs), but they are highly dependent on the chosen evolutionary parameters. A self-adaptive evolutionary algorithm (SAEA) is a modification of a genetic algorithm aimed at solving the parameter fitting problem. In a classical GA, parameter tuning is performed before it starts, and the parameters themselves remain unchanged throughout the algorithm's operation, which can make it difficult to find the best solution. Finding optimal parameters is critical to the quality of the GA, but is often time and resource consuming. An approach to solving the travelling salesman problem is proposed in which the parameters of the SAEA, such as mutation probability, ratio of offspring to new specimens, type of crossing over and type of selection are optimised during its operation. This is achieved by evaluating the current success or failure of the evolutionary process through fuzzy logic.
1. Введение
Генетические алгоритмы (ГА) — это алгоритмы поиска и оптимизации, основанные на принципах естественного отбора, эволюции. Задачи оптимизации заключаются в нахождении минимума или максимума заданной, целевой функции. При работе генетического алгоритма создается ряд решений, популяция, соответствующая рассматриваемой задачи, после чего наиболее хорошие решения порождают потомков путём рекомбинации и, иногда, мутации своих генов, из-за чего алгоритмы и называются эволюционными . Процесс продолжается на протяжении многих поколений. Решение — это значение пригодности для каждой особи популяции, которое зависит от целевой функции. Каждое из возможных решений называется «хромосомой». Члены популяции оцениваются по функции приспособленности и получают баллы в зависимости от степени приспособленности .
Задача коммивояжера — комбинаторная задача оптимизации, целью которой является нахождение оптимального критериям маршрута между точками, которые принято называть городами. Это известная и хорошо изученная NP-полная задача, что делает её хорошим выбором для измерения эффективности новых экспериментальных эвристических алгоритмов оптимизации. Задача коммивояжера несмотря на то, что известна с 1930 года , всё ещё не теряет свою актуальность в современном мире, напротив, появляется всё больше различных модификаций этой задачи , . Существует несколько причин, по которым ГА хорошо подходят для решения задачи коммивояжера. Во-первых, они эффективны в нахождении не лучших, но оптимальных решений за приемлемое время. Во-вторых, у NP-полных задач огромное пространство поиска решений и ГА эффективно исследуют это пространство, так как поддерживают целую популяцию решений, а не проверяют по одному за раз. Также принципы кроссинговера позволяют ГА не терять найденные хорошие решения и в то же время не застревать в локальных оптимумах благодаря мутациям и появлению новых особей , . Две разных задачи коммивояжера могут сильно отличаться друг от друга из-за особенностей расположения городов в пространстве, их количества, дополнительных условий и модификаторов. Это приводит к тому, что эволюционные параметры ГА необходимо настраивать отдельно для каждой задачи. Для решения этой проблемы был разработан самоадаптирующийся эволюционный алгоритм (САЭА) . Его особенность заключается в том, что такие параметры как вероятность мутации, соотношение потомков и новых особей, тип кроссинговера и тип отбора изменяют своё значение в процессе работы алгоритма. Процесс изменения параметров реализован с помощью нечёткой логики. Нечёткая логика — это набор нестрогих правил, которые расширяют стандартную булевскую логику. Она формализована с помощью теории нечетких множеств, где элементы могут иметь степени принадлежности к множеству, а не четкую принадлежность, как в классической теории множеств. Нечеткая логика обеспечивает основу для приблизительного рассуждения на основе лингвистических переменных и правил ЕСЛИ-ТО, позволяя выполнять вычисления с неточной или расплывчатой информацией .
2. Методы и принципы исследования
Для проведения вычислительного эксперимента была выбрана задача коммивояжера со следующей постановкой задачи :
Пусть — множество городов.
Пусть — стоимость (расстояние) перемещения из города
в город
.
Пусть переменная решения — двоичная переменная, такая что:
Цель — минимизация общей стоимости тура:
с учётом следующих ограничений:
Основная цель ГА в задаче коммивояжера — определить гамильтонов цикл минимального веса в взвешенном полном графе. При работе ГА возможное решение задачи кодируется в особи как хромосома, которая представляет из себя перестановку множества городов
. Хромосома имеет вид
и представляет собой упорядоченный тур, посещающий каждый город ровно один раз. ГА работает с популяцией
в поколении
, определяемой как множество из
особей:
, где
— размер популяции. Качество или пригодность каждой отдельной особи определяется целевой функцией
, которая вычисляет общую длину тура, закодированного
. Эта функция определяется следующим образом :
Эволюционный процесс проходил через поколения посредством итеративного применения генетических операторов, в первую очередь отбора, кроссинговера и мутации. Механизмы отбора выбирали родительских особей из на основе их значений приспособленности, тем самым сохраняя более удачные решения. Были реализованы следующие операторы отбора: турнирный отбор и метод колеса рулетки. В качестве операторов кроссинговера использовались одноточечный и равномерный . Было реализовано два вида мутаций: мутация обменом меняла позиции двух случайно выбранных городов в перестановке; обратная мутация меняла порядок городов в случайно выбранной подпоследовательности на обратный.
Основанная идея САЭА заключается в преодолении проблемы ручного выбора оптимальных эволюционных параметров, что перечислены выше. Вместо использования фиксированных параметров САЭА динамически корректирует их во время выполнения на основе получаемой от популяции обратной связи. Реализованный алгоритм имел следующий принцип работы. Создавались три стартовых популяции, которые в дальнейшем, для избегания путаницы с популяциями, создаваемыми во время работы алгоритма, будут называться группами. Развитие популяций в каждой группе проходило одновременно, а их сравнение являлось важной частью в механизме принятия решений. Каждая группа имела независимый набор параметров: шанс мутации, тип мутации, тип отбора, вероятность того, будут отобранные особи скрещены или перенесены в новое поколение, размер турнирного отбора, тип кроссовера. Адаптация параметров осуществлялась путем изучения внутреннего состояния популяций, в частности, их характеристик конвергенции. Конвергенция — формирование похожих признаков у неродственных групп организмов, обитающих в сходных условиях. Использовались две метрики конвергенции: фенотипическая и генотипическая . Фенотипическая конвергенция определялась стандартным отклонением значений приспособленности в популяции. Низкое стандартное отклонение указывало на большую схожесть фенотипа особей, то есть, на схожее качество решений. Генотипическая конвергенция оценивалась частотой наиболее распространенного генотипа хромосомы в популяции. Высокая конвергенция указывала на снижение разнообразия на уровне структуры решения. Механизм адаптации различался в разных группах. Первая и вторая группы использовали механизм принятия решений на основе нечеткого вывода для управления параметрами. Этот механизм получал текущие фенотипические и генотипические метрики конвергенции соответствующей популяции в качестве входных данных. На основе предопределенного набора нечетких правил, которые кодировали эвристические знания о связи между состоянием конвергенции и желаемыми корректировками параметров, механизм вычислял рекомендуемые изменения для каждого компонента вектора параметров. При этом приоритетом популяций первой группы являлся поиск новых решений, а приоритетом второй группы являлась оптимизация найденных хороших решений. Корректировки для непрерывных параметров были аддитивными, в то время как корректировки для категориальных параметров работали подобно переключателю между разными типами. Третья группа реализовывала случайную стратегию исследования для своих параметров. В каждом поколении весь список параметров для этой группы повторно выбирался случайным образом из предопределенных границ параметров. Это давало следующие преимущества: обеспечивало непрерывное исследование пространства параметров, потенциально обнаруживая эффективные комбинации параметров, пропущенные механизмом принятия решений, и действовало как динамический контроль, предотвращая постоянное попадание алгоритма в потенциально неоптимальные конфигурации параметров.
Механизм принятия решений реализован на основе правил нечёткой логики .
Пусть:
: четкое входное значение для фенотипической конвергенции.
: четкое входное значение для генотипической конвергенции.
: четкое входное значение для типа группы.
функции принадлежности для
, «Низкое», «Среднее», «Высокое» соответственно.
функции принадлежности для
, «Низкое», «Среднее», «Высокое» соответственно.
функции принадлежности для
, «Группа 1» и «Группа 2» соответственно.
выходные переменные, представляющие изменение вероятности мутации, вероятности кроссовера, размера турнира, индекса оператора отбора, индекса оператора кроссовера и индекса оператора мутации соответственно.
функции принадлежности для выходных нечетких множеств, которые обозначают «Увеличить немного», «Уменьшить немного», «Без изменений», «Увеличить», «Уменьшить» соответственно.
функция нечеткой импликации, определяющая форму выходного нечеткого множества на основе силы срабатывания правила α.
функция агрегации, объединяющая нечеткие множества из всех правил для заданной выходной переменной.
функция дефаззификации, вычисляющая четкое выходное значение методом центроида.
Для каждого правила изначально вычислялась сила срабатывания правила
на основе входных значений и имеющихся функций принадлежности. Затем для каждой выходной переменной, затронутой правилом, определялось нечёткое выходное множество .
Правило 1, которое увеличивало сходимость для первой группы.
Сила срабатывания: .
Выводы:
Правило 2, которое увеличивало разнообразие фенотипов в первой группе.
Сила срабатывания:
Выводы:
Правило 3, которое помогало второй группе преодолевать слишком высокую генотипическую и фенотипическую конвергенции.
Сила срабатывания:
Выводы:
Правило 4, которое помогало второй группе преодолевать слишком высокую фенотипическую конвергенцию.
Сила срабатывания:
Выводы:
Правило 5, которое выполнялось при отсутствии необходимости во вмешательстве.
Сила срабатывания:
Выводы: никакие параметры не изменяются
Для каждой выходной переменной агрегированный нечеткий набор получался путем объединения подразумеваемых выводов из всех правил, влияющих на этот параметр. Для примера, агрегирование вероятности мутации имело следующий вид :
Четкое выходное значение вычислялось с использованием дефаззификации :
В частности, с использованием метода центроида , где интеграл брался по всему диапазону возможных значений
для
.
3. Вычислительный эксперимент
Целью вычислительного эксперимента была проверка эффективности разработанного алгоритма в сравнении с классическим ГА. Выбранные числовые параметры не моделировали какой-либо реальный процесс. Их подбор основывался на том, чтобы результаты имели значимость в статистическом анализе. Вычислительный эксперимент проводился со следующими параметрами:
- Количество независимых запусков — 50.
- Количество созданных поколений — 1000.
- Стартовый размер популяции — 50.
- Способ создания стартовой популяции — случайное заполнение.
Для стандартного ГА:
- Метод отбора — турнирный отбор.
- Размер турнира — 5.
- Оператор кроссовера — одноточечный.
- Коэффициент кроссинговера — 0,8.
- Оператор мутаций — мутация обменом
Для САЭА:
- Количество групп — 3.
- Доступные операторы отбора — турнирный отбор и метод колеса рулетки.
- Доступные операторы мутаций — мутация обменом и обратная мутация.
- Интервал шанса мутации — [0,01; 0,5].
- Интервал коэффициента кроссинговера — [0,5; 0,95].
- Интервал турнира — [2; 10].
Решение eil51 задачи показало следующий результат:
- Точное известное решение — 426.
- Решение САЭА — 442,38.
- Решение ГА — 606,14.
Результат эксперимента с теми же параметрами, за исключением количества поколений, которое было снижено до 500:
- Решение САЭА — 475,22.
- Решение ГА — 672,8.
При дальнейшем снижении числа поколений до 200 получен следующий результат:
- Решение САЭА — 502,92.
- Решение ГА — 782,54
На основании полученных данных был сделан вывод, что явным преимуществом САЭА является быстрое нахождение не идеального, но хорошего решения. При уменьшении количества популяций САЭА теряет качество своих результатов с заметно меньшей скоростью, чем ГА.
На рис. 1 можно увидеть визуализацию работы алгоритмов и сравнить скорость поиска решения САЭА с ГА.
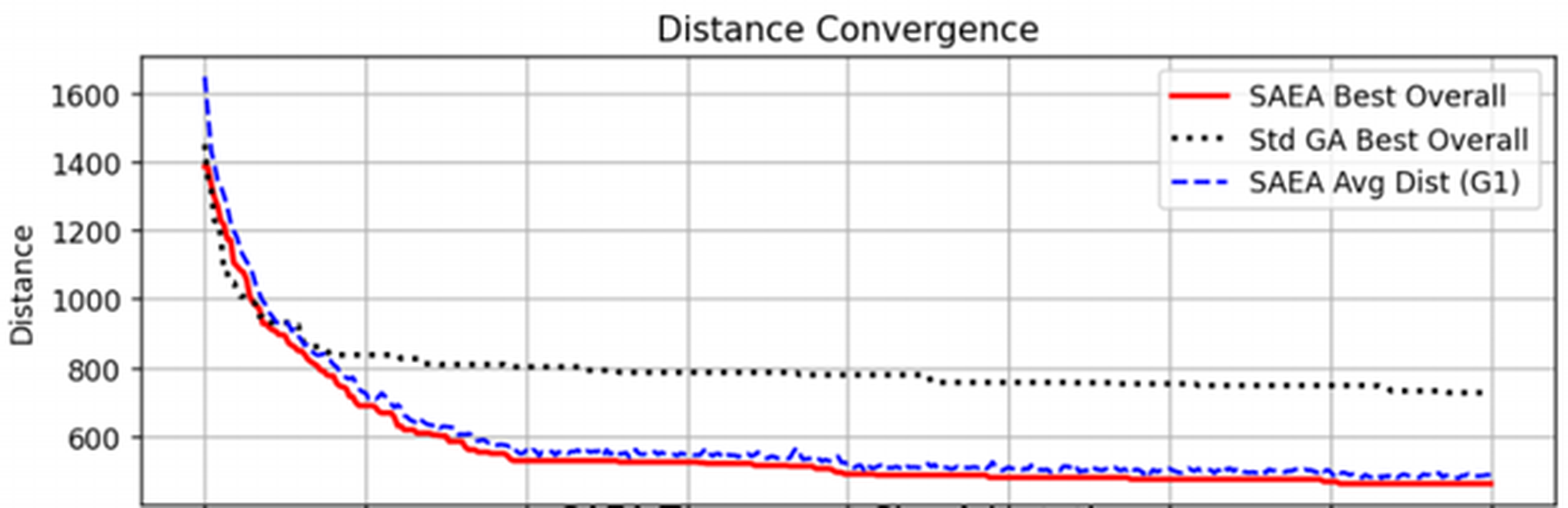
Рисунок 1 - Зависимость значения целевой функции от номера популяции
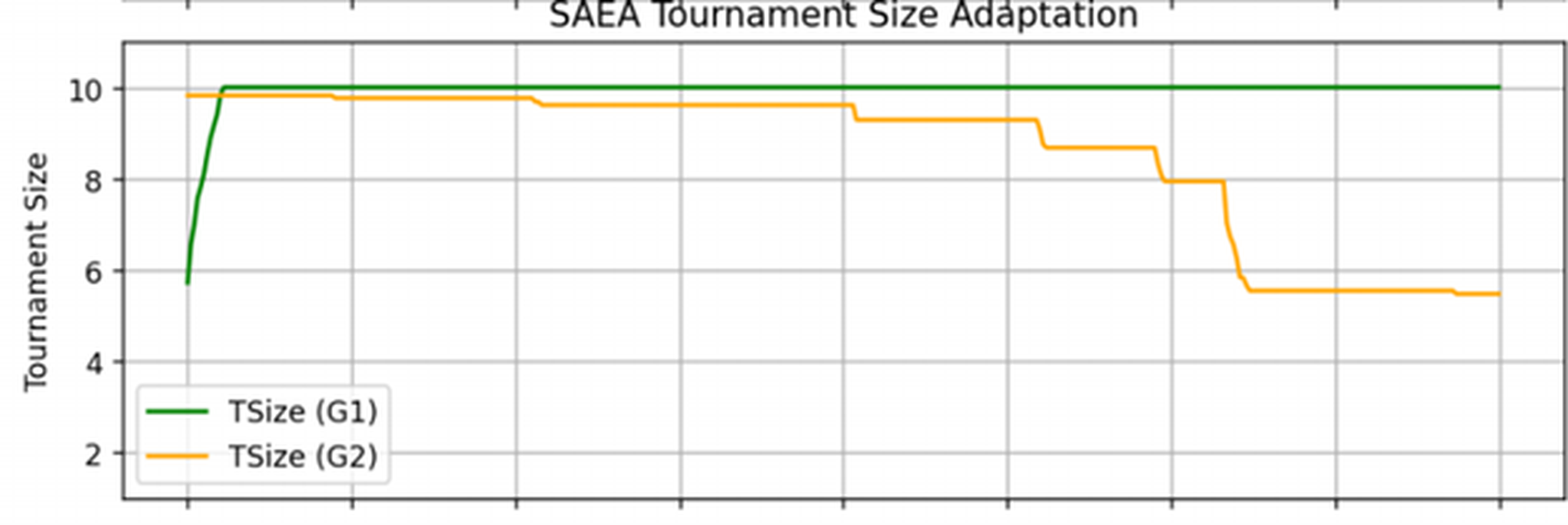
Рисунок 2 - Зависимость размера турнирной таблицы от номера популяции
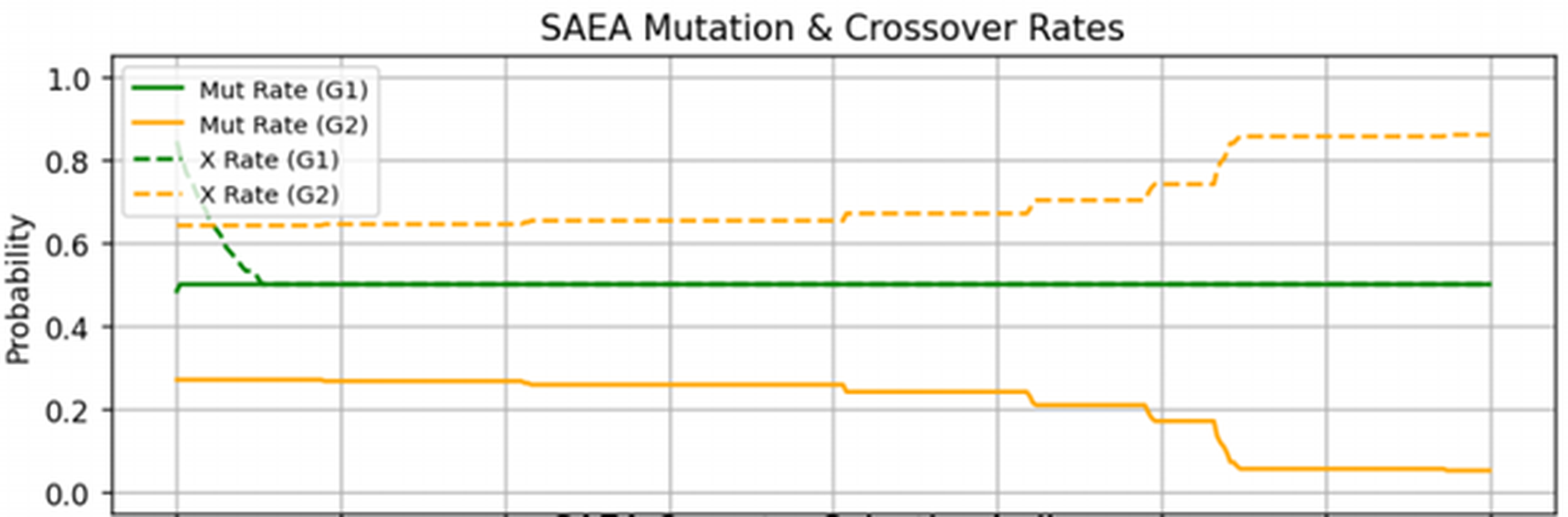
Рисунок 3 - Зависимость вероятности мутации и коэффициента кроссинговера от номера популяции
4. Заключение
Был рассмотрен самоадаптирующийся эволюционный алгоритм, являющийся модификацией генетического алгоритма. Использование правил нечёткой логики позволило реализовать механизм принятия решений, способный на основании анализа успешности или неуспешности проходящего эволюционного процесса вносить изменения в эволюционные параметры, которые обычно являются фиксированными. Благодаря этому результат САЭА ближе к точному решению, чем результат ГА. Так же САЭА менее чувствителен к сокращению числа популяций в эволюционном процессе, чем ГА.
В качестве дальнейшего развития планируется модифицировать САЭА для работы с усложнёнными задачами коммивояжера с дополнительными ограничениями; реализовать методы, позволяющие ещё сильнее сократить необходимость какой-либо ручной настройки САЭА перед его запуском независимо от типа задачи; совместить САЭА с другими модифицированными ГА, например, с социальным или хронологическим.
