Calculation of concentration profile parameters in ion doping by finding the minimum of the target function by the Davidon-Fletcher-Powell method
Calculation of concentration profile parameters in ion doping by finding the minimum of the target function by the Davidon-Fletcher-Powell method
Abstract
This work is dedicated to the application of the Davidon-Fletcher-Powell method to find the minimum of the target function in the calculation of concentration profile parameters during ion doping. A two-layer structure (SiO2 + Si) as the closest to practical silicon technology was taken as a mathematical model of the target during ion implantation. The Birsak diffusion model was used in the modelling of ion implantation. To carry out the simulation and optimization, based on the mathematical model of ion implantation, the Biersack diffusion theory and the Davidon-Fletcher-Powell method, a program was written, and the corresponding calculations were carried out. The developed algorithm has shown its performance and the possibility of using it to find the initial parameters for ion doping.
1. Введение
Ионная имплантация в последние годы стала одним основных методов легирования материалов при производстве структур БИС и СБИС
, , , , . Данная технология подразумевает, что заряженные частицы управляемого потока легирующей примеси бомбардируя твердое тело, внедряются, изменяя его электрофизические, оптические и другие свойства. Среди основных достоинств метода ионного легирования можно выделить возможность точно и воспроизводимо дозировать внедряемую примесь и получать высокую точность заданного профиля.Процесс ионной имплантации часто проводится через диэлектрические слои. Для этого существуют различные причины:
- избежание загрязнения полупроводника;
- регулирование распределения глубины;
- исключение образования каналов;
- технологические причины.
Для того чтобы точно рассчитать распределение примеси по глубине в многослойной структуре, требуется решение транспортных уравнений.
Целью данной работы является нахождение начальной дозы легирования и начальной энергии иона для заданного профиля при проведении ионной имплантации. Расчеты предполагается проводить на основе диффузионной теории Бирсака при использовании оптимизации методом Давидона-Флетчера-Пауэла.
2. Профили распределения двухслойных мишеней
Для предотвращения загрязнения кремния, создания рассеивающего слоя или регулирования глубины залегания ионов, легирование примеси проводится через тонкие маскирующие слои, такие как SiO2 Si3N4. Чтобы точно вычислить распределение примеси по глубине, можно воспользоваться методом Монте-Карло. Но это требует больших затрат машинного времени.
Для практических потребностей кремниевой технологии можно использовать простую модель, предложенную в и пригодную для материалов, имеющих близкие средние атомные номера и массы. Это условие выполняется для большинства композиций используемых с кремнием, например, SiO2, Si3N4, Al2O3 и т.д. На рис.1 приводится схематическое изображение этой модели.
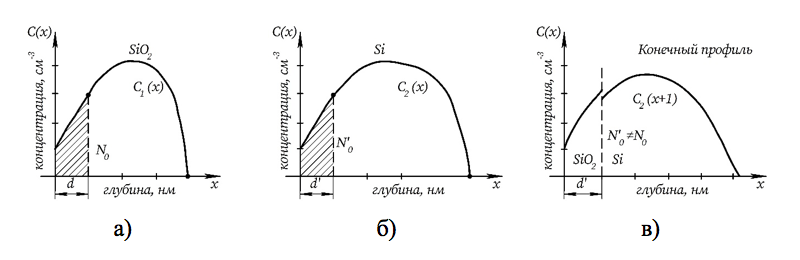
Рисунок 1 - Схематическое изображение численной модели для имплантации в многослойные структуры
Примечание: C1(x) – профиль концентрации в материале 1 (SiO2) [маска];
C2(x) – профиль концентрации в материале 2 (Si) [подложка];
N0 – количество ионов примеси на глубине
где
Ошибка при использовании (1) равна
где
Выражение (1) получается из распределения концентрации примеси в толстом слое окисла преобразованием плотности с помощью масштабирующего
Поскольку форма профиля концентрации примеси в кремнии обычно важнее, чем в слое окисла, то для тонких слоев и произвольного профиля распределения можно использовать следующие соотношения:
Данная модель дает хорошие результаты, если ионы концентрируется во втором слое.
Для уточнения профиля распределения в обоих предельных случаях (случаи толстого и тонкого слоев) может быть проведено дальнейшее усовершенствование модели.
С этой целью рассчитывать профиль распределения
Затем определяется профиль распределения
Окончательный профиль распределения состоит из профиля
3. Диффузионная теория Бирсака
В теории, предложенной Бирсаком
, , процесс замедления имплантируемых ионов описывается диффузионной моделью, в которой вычисляется средний поправочный косинус ионной траектории во время замедления. Поэтому ионы изменяют направление движения после каждого столкновения, они будут в среднем все больше и больше отклоняться от своего первоначального направления. В свою очередь, потери энергии при ядерных столкновениях, обусловленных передачей импульса от иона, не имеют однозначной связи с угломЕсли теперь рассмотреть функцию распределения W полярного угла
Для вычисления длины проективного пробега нет необходимости явно проходить функцию W, а достаточно вычислить среднее значение направляющего косинуса
Связь между τ и энергетическими потерями находится с помощью соотношения Эйнштейна и имеет вид:
где М1 и М2 – масса иона и мишени, Е – энергия налетающей частицы,
Это приводит к следующим уравнениям для пробега R и проектного пробега Rp:
Каждый прямолинейный элемент траектории иона проецируется на ось x умножением его длины на направляющий косинус. Длину проективного пробега можно вычислить нахождением τ из (6) и последующей подстановкой в (7). Однако алгоритм, разработанный Бирсаком, дает возможность вычислить
Уравнения (9)-(12) легко программируются для быстрых итерационных вычислений
Для Sn можно использовать аналитическое приближение, например:
где
4. Метод Давидона-Флетчера-Пауэлла
Метод Давидона-Флетчера-Пауэлла (ДФП) основан на использовании соотношений
Однако в данном случае не требуется на каждом шаге вычислять обратный гессиан
Начнем поиск из начальной точки x0, взяв в качестве начальной матрицу Н0 (обычно единичную матрицу, хотя в этом случае может подойти любая симметричная положительно определенная матрица). Итерационная процедура может быть представлена следующим образом (вместо g(xi) удобнее gi):
1. На шаге i имеются точка xi и положительно определенная симметричная матрица Hi.
2. В качестве направления поиска взять направление
3. Чтобы найти функцию
4. Положить
5. Положить
6. Найти
Из соотношения
7. Положить
8. Обновить следующую матрицу Н следующим образом:
где
9. Увеличить i на единицу и вернуться на шаг 2.
Метод ДФП использует как идеи Ньютона-Рафсона, так и свойство сопряженных направлений, и при применении для минимизации квадратичной функции n переменных он сходится не более чем за n итераций. Это весьма мощная оптимизационная процедура, очень эффективная при оптимизации большинства функций независимо от того, квадратичны они или нет , , . На рис. 2 представлена блок-схема метода.
5. Результаты моделирования и оптимизации
Для проведения моделирования и оптимизации, на основе представленных выше математической модели ионной имплантации, диффузионной теории Бирсака и метода Давидона-Флетчера-Пауэлла была написана программа, позволяющая автоматически проводить расчеты. Проверка работоспособности, полученной программы проводилась с помощью контрольного примера, позволяющего получить заданный профиль с приращением во всех направлениях, имея следующие параметры:
· энергия иона – 87 кэВ;
· доза легирования – 50000000 1/мкм2.
Далее задавая различные ошибки начальных параметров было рассчитано за сколько итераций и насколько точно с помощью метода Давидона-Флетчера-Пауэлла будут получены правильные (оптимальные) значения параметров, соответствующие заданному профилю. Результаты работы программы представлены в Табл.1.
Анализ полученных результатов позволяет сделать следующие выводы. Все точки которые были заданы в качестве начальных, показали хорошие результаты работы программы. Средняя погрешность по энергии составила 0,033%. Средняя погрешность у дозы легирования 1,012%. В процессе проверки не были замечены никакие закономерности в увеличение или уменьшении погрешностей, т.к. погрешность в дозе легирования почти в 1,5% была замечена сразу же в первой точке, но потом на протяжении 10 точек погрешность была меньше 1%, а иногда меньше 0,1%. Потом резкий скачок до 3,6% и опять в течении 5 точек очень низкая погрешность. В измерении №15 (ошибка в задании параметров составляла 50%) программа нашла точки, наиболее точно соответствующие необходимому значению. При задании ошибки в 100% программа дала погрешность по дозе почти 9%, поэтому дальнейшее увеличение ошибки и проверка программы не проводилась.
![Блок-схема алгоритма оптимизации методом Давидона-Флетчера-Пауэлла [18]](/media/images/2024-10-06/91a3795a-7eb1-4b4f-9381-d96667364948.png)
Рисунок 2 - Блок-схема алгоритма оптимизации методом Давидона-Флетчера-Пауэлла [18]
Таблица 1 - Результаты поиска параметров ионного легирования
Ошиб. в % | № изм. | Кол-во итераций | Нач. энергия, КэВ | Нач. доза, 1/мкм2 | Получ. энергия, КэВ | Получ. доза, 1/мкм2 | Погрешн. энергии, % | Погрешн. дозы, % |
10 | 1 | 38 | 78,3 | 45∙107 | 87,021 | 49267297,74 | 0,024 | 1,465 |
2 | 25 | 95,7 | 45∙107 | 87,009 | 49852166,06 | 0,010 | 0,296 | |
3 | 35 | 78,3 | 55∙107 | 87,001 | 49992501,66 | 0,001 | 0,015 | |
20 | 4 | 26 | 104,4 | 40∙107 | 86,995 | 50097496,95 | 0,006 | 0,195 |
5 | 37 | 104,4 | 60∙107 | 87,014 | 49805852,08 | 0,016 | 0,388 | |
6 | 28 | 69,6 | 60∙107 | 86,998 | 50104233,76 | 0,002 | 0,208 | |
7 | 52 | 69,6 | 40∙107 | 87,004 | 49937067,8 | 0,005 | 0,126 | |
30 | 8 | 13 | 113,1 | 35∙107 | 87,005 | 49633478,74 | 0,006 | 0,733 |
9 | 33 | 113,1 | 65∙107 | 87,001 | 49984451,59 | 0,001 | 0,031 | |
10 | 37 | 60,9 | 65∙107 | 86,993 | 50120982,28 | 0,008 | 0,242 | |
40 | 11 | 45 | 52,2 | 30∙107 | 87,016 | 49933663,52 | 0,018 | 0,133 |
12 | 36 | 121,8 | 30∙107 | 87,114 | 48190182,33 | 0,131 | 3,620 | |
13 | 50 | 121,8 | 70∙107 | 86,996 | 50067333,81 | 0,005 | 0,135 | |
14 | 29 | 52,2 | 70∙107 | 86,99 | 50186265,96 | 0,011 | 0,373 | |
50 | 15 | 47 | 43,5 | 25∙107 | 87,001 | 49999412,33 | 0,001 | 0,001 |
16 | 33 | 130,5 | 25∙107 | 87,002 | 49968148,13 | 0,002 | 0,064 | |
17 | 29 | 130,5 | 75∙107 | 86,991 | 50181321,21 | 0,010 | 0,363 | |
18 | 36 | 43,5 | 75∙107 | 86,924 | 50571855,6 | 0,087 | 1,144 | |
75 | 19 | 216 | 152,25 | 125∙107 | 87,062 | 48745908,84 | 0,071 | 2,508 |
20 | 29 | 152,25 | 87,5∙107 | 86,966 | 50117790,97 | 0,039 | 0,236 | |
100 | 21 | 15 | 174 | 100∙107 | 87,21 | 45515288,85 | 0,241 | 8,969 |
| Средняя погрешность | 0,033 | 1,012 | |||||
6. Заключение
Исходя из представленных выше данных можно сделать вывод о возможности использовании метода Давидона-Флетчера-Пауэлла для поиска оптимальных параметров ионного легирования. Разработанная Программа показала свою работоспособность, а предложенный метод оптимизации свою адекватность и пригодность для решения поставленной задачи. Однако при проведении расчетов следует учесть, что наименьшая погрешность получается при задании параметров с ошибкой менее 100%. Данный факт указывает на необходимость проведения начальной подготовки перед проведением моделирования и расчетов с цель получения наилучшего результата.
